オンラインセミナーシリーズ「女子中高生のための『数理・情報・AI』最前線！」第4回を、2022年12月8日（木）に開催しました。今回は二人の研究員がお話をしました。篠田万穂先生は研究している力学系理論やエルゴード理論という数学の分野について、また、竹内愛理先生はおなじく数学的ビリヤードという数学の分野について、それぞれイメージのわく図も交えて紹介。数学の進路に向け、女子中高生たちの背中を後押しするようなメッセージもありました。
「数学は科学の言葉」と感じ、数学の道へ
カオス現象を数学的に理解しようとする理論が力学系理論です。チョウの小さな羽ばたきが時間発展とともにハリケーンを起こすことがあることをいう「バタフライ効果」はカオス現象の例です。
中高生時代、家族・学校・バレエの三つの居場所が私にはありました。嫌なことがあっても、別の場所でいいことがあったりして、複数の居場所があると人生は楽しくなると感じました。
数学については中学のとき、「この二つの直線に交点はあるか」という幾何の問題が、「連立方程式に解はあるか」という代数の問題と同じだと理解ができ、「おもしろいかも！」と思いました。さらに高校のとき、物理で習った円運動を三角関数の微積分で表せることがわかり、「数学は科学の言葉だ」と実感しました。これが数学の進路を選ぶ理由の一つになりました。とはいえ具体的な進路は明確ではなかったので、2年生から学科を選ぶことができる慶應義塾大学理工学部に入学しました。1年生のときに学んだ数学の行列式の定義におもしろさを感じて、2年生からは数学科に進みました。数学は、女性が少なかったのですが、友だちと曲線の面積を積分を使って求める話で盛りあがったり、女性の先生が楽しそうに研究している姿を見たり、またメンターの方が親身になって相談に乗ってくれたりして、楽しく数学を学ぶことができました。
大学4年に研究室に配属となりますが、私は力学系理論の分野を選びました。配属前、担当の先生から「法則が単純でも時間発展が複雑にあることがある」といった話を聞いて興味をもったからです。
力学系理論で時間発展を表現する
力学系理論について説明します。xnを関数fで計算すると時刻xn＋1での状態が決まるというモデルがあります。xn＋1 ＝ f（xn）と表せます。実はみなさんもこのモデルの簡単なものを使って未来予測をしているのです。たとえば「10年後あなたは何歳か」という問題は、xn＋1 ＝ xn＋1で表せます。ここでの時間発展のルールは f（x）＝x＋a という等差数列の式になります。別の見方では y＝x＋a のグラフにもなり、初期値 x0 の点から対応するf（x0）点へといったように辿っていくと、時間発展をグラフでも理解できます。
また「大腸菌が分裂して倍になる」といった事象を、xn＋1 ＝ 2xn と表せます。より一般化すると時間発展のルールを f（x）＝ rx という等比数列の式で表せます。グラフでは y=rx と y＝x の二つの直線で表され、x0の点から両直線上の点を辿っていくと、時間発展をグラフでも理解できます。
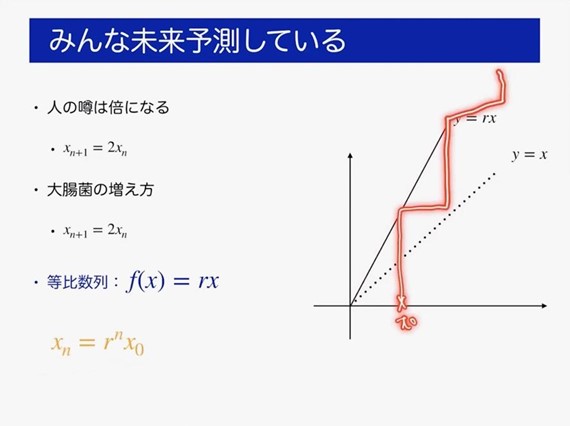
この大腸菌の式に、「個体数がMになったら、増えすぎてぜんぶ死んでしまう」という環境要因を表す（M−xn）の項を入れて、xn＋1 ＝ rxn（M−nx）とし、さらにMを1としたときの yn＋1 ＝ Ryn（1−yn）を考えます。このとき時間発展のルールだけを抜き出してみると、f（x）＝ Rx（1−x）＝ −Rx2＋Rxという式となり、これをロジスティック写像の式といいます。
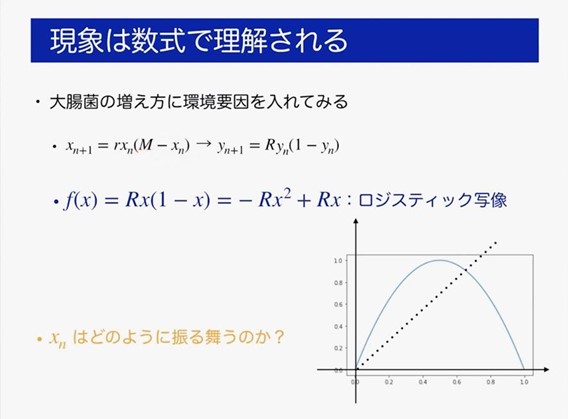
ロジスティック写像での時間発展をグラフに描いてみます。さきほどの等差数列や等比数列より複雑で、とくにR＝4ではとても複雑に見えます。本当に複雑なのかを、距離について絶対値 |x−y| で調べたり、微分について傾きf'（x）で調べたり、数学的構造をもとに調べます。現象は数式で理解されるともいえます。調べていくと、R＝4のとき、「x0, y0が近ければ xn, ynも近い」はまちがいであることや、あるx0の軌道は定義域の「いたるところ」にあることなどがわかります。
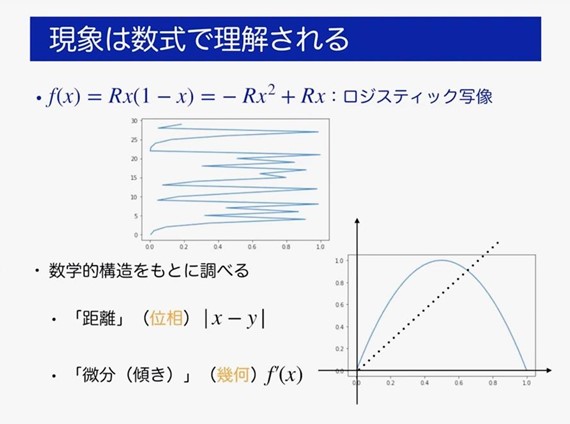
「ほとんどすべての」すべての初期点0に対してその軌道はランダムに振る舞うように見えますが、初期点により大きく振る舞いが異なるものをどう理解したらよいでしょうか。そのためには統計的な量を見ていきます。
たとえば、xnがとりうる領域に集合Aを設け、初期点x0からx1、x2、x3……とプロットしてAに入る数を数えたり、また0.0から1.0にかけての区間を分割して入った数の分だけグラフの棒を高くする作業を無限回くりかえし、下に凸の曲線になることを確かめたりといったことです。
エルゴード理論で確率的に現象を調べる
こうした作業を厳密におこなうためにエルゴード定理を使います。この定理は、時刻のnを無限のような長時間にすると、時間的な平均は空間的な平均と一致することを指すものです。時間平均から確率を出して、確率を調べることで力学を理解しようとします。
こうして、確率の概念を使ってカオス現象を調べるエルゴード理論の研究もしています。
数学は「あらゆるところ」に使われている
私はいまドイツのアウクスブルク大学でポスドク（研究員）として数学を研究しています。アウクスブルクはミュンヘンに近い、きれいな街です。大学のキャンパスには川が流れています。
さて、数学はどんなところに使われているでしょうか。その答えは「あらゆるところ」です。数学の周辺は世界であるといえます。数学の分野には大きく、代数、幾何、解析、確率、統計、計算科学、集合、論理などがあります。
個人的に好きな数学の応用先の一つが建築です。建築を支える、強力なツールに幾何があります。直接は測れないものを測ろうとするなかで、幾何学の代表的なユークリッド幾何学が発展したといわれています。ほかにも数学の応用先には、情報セキュリティ、電子工学、古典力学、量子力学、人工知能などさまざまあります。数学がどのように世界とつながっているかを知りたい方は、「数理女子」というサイトの「世界は数学であふれている」というページを見てみてください。
数理女子Webサイト・「世界は数学であふれている」へのリンク
「世界は数学の言葉で語られている」
高校時代は、物理と科学史にハマりました。イタリアの物理学者ガリレオ・ガリレイ（1564-1642）の「世界は数学の言葉で語られている」という言葉を知り、「自然が宗教で理解されていた時代でもガリレイは未来を見ていたんだ」「数学を理解することが世界を理解することになる」と感じました。
ガリレイと同時代の天文学者にドイツのヨハネス・ケプラー（1571-1630）がいます。天体力学の分野で、惑星は太陽のまわりを楕円軌道でまわるという「ケプラー運動」を導きだしました。ケプラー運動は、最初の位置がわかればその後の位置を計算できることを意味する可積分という性質を持ちます。
一方、惑星と太陽に、三つ目の天体として小惑星を加えると「制限三体問題」として扱われることとなり、可積分でなくなります。さらに制限を加えた「円制限三体問題」では、五つの平衡点からなるラグランジュ点が存在することが数学的に証明されています。実際、宇宙観測によって、数学的に示された平衡点の空間に小惑星群があるとわかり、理論と現実が一致しました。
三つ目の天体にごく小さいという制限がないと、三つの天体の軌道はとても複雑になります。これに対し、1993年に8の字の安定周期解が証明されました。さらに2018年には1000以上、2021年には1万3315の周期解が発見されています。なお三体問題は最近、劉慈欣が書いたサイエンスフィクション『三体』でも題材になっています。
近年も進展の多い「数学的ビリヤード」を研究
研究テーマの「数学的ビリヤード」について紹介します。長方形の平面上を球が転がり、台や壁による摩擦がある現実のビリヤードに対し、数学的ビリヤードでは平面でなくてもよく、どんな形でもよく、摩擦を考えません。壁に物体がぶつかったとき入射角と反射角が等しくなるという反射の法則を満たします。
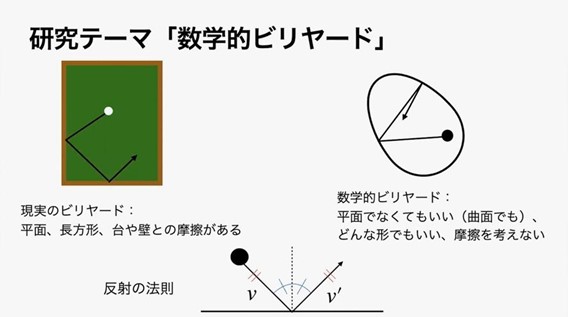
数学的ビリヤードは光学に応用されます。壁が鏡になっている部屋を光源一つで照らせるかというイルミネーション問題や、水滴内の反射を経て虹の現れる角度が40〜42度となる虹の数学的原理が数学的ビリヤードを考えることで説明できます。
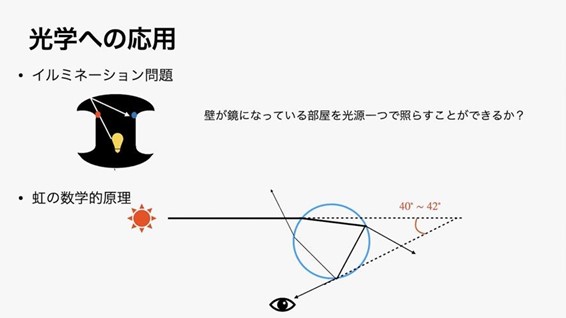
私が数学的ビリヤードで研究している対象は主に二つあります。
一つは「規則的ビリヤード」です。球の軌跡が最初の位置に戻るという周期的、またはそれに近い準周期的なふるまいをするかとなる可積分なビリヤードです。もう一つは、「カオス的ビリヤード」です。カオス的なビリヤードは初期位置をすこし変えるだけでその後の軌道が大きく変わるという性質を持ちます。たとえば、トーラスというドーナツの表面のような曲面から円板を除いたものの上で定義された数学的ビリヤードの挙動はカオス的になります。
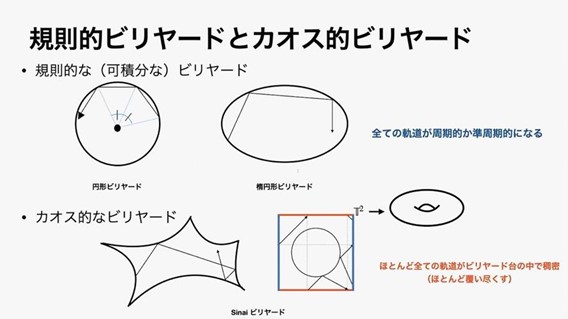
私はいま「力学的ビリヤード」の問題を研究しています。これは例えば、ケプラー運動に従う惑星の軌道上に、大きな反射壁を建設したら惑星がどのような軌道になるかといった問題を考えます。オーストリア出身の物理学者ルートヴィッヒ・ボルツマン（1844-1906）は1868年に、この力学的ケプラービリヤードはエルゴード的である、つまり規則的でないと予想しました。ところが近年の研究でこれが覆り、規則的であると判明しました。私達の研究では、ケプラー問題に楕円の反射壁の存在を足すと、惑星の軌道はやはり規則的になることを示しました。
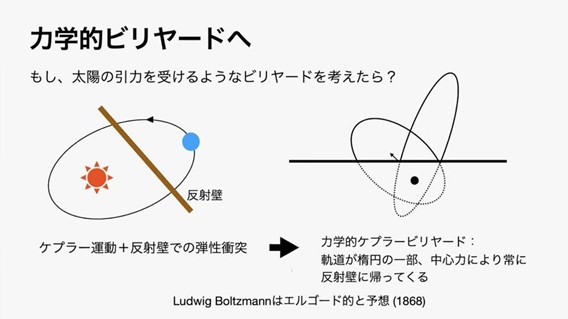
数学的ビリヤードをめぐり、「可積分な閉じたビリヤード系は円形か楕円形だけである」とするバーコフ・ポリツキー予想があります。最近、部分的に証明されて話題になりました。私たちは、「可積分な閉じたケプラービリヤード系は円形か楕円形だけである」という仮説を立てています。仮説を立てることで、「ほかの力学的ビリヤード系ではどうか」「次元を上げて3次元にしたらどうか」と、新たな疑問が浮かんできます。
数学者って……怖くないよ！
数学者や数学科を別の世界のものと考え、怖いと思っている人もいるかもしれません。これはかつて私も思っていたことです。
いま私が数学の世界に入ってみて言えるのは、数学者はみんな数学が好きであり、わからないことを尋ねると喜んで教えてくれる文化があるということです。知的好奇心が強く、数学の応用面よりむしろ数学そのものが好きという人は多くいます。数学の議論は正しいことの積み重ねを前提としているので、まちがいを見つけたときは指摘や訂正をします。私のまわりには女性の数学者が多く、またアニメ・漫画・ゲーム好きの数学者も多くいます。今はすごく楽しくて、「怖くないよ！」と皆さんに伝えたいです。
