オンラインセミナーシリーズ「女子高生のための『数理・情報・AI』最前線！」第3回を2022年12月1日（木）に開催しました。今回は数学の二つの視点をみなさんと分かちあいました。関坂（山本）宏子先生が、自然界にも見られるパターン形成の理解に役立てるという視点から非線型偏微分方程式の有用性などを紹介。また学生の伊藤歌那さんが、メタ的視点から数学の論理性などを紹介しました。
大学生時代に転学し、数学研究の道へ
私は、数学の非線型偏微分方程式、とくに、どのように生物が形づくられるかなどと関連のある反応拡散系に興味をもって研究しています。
高校時代に数学が好きになり、数学の高校教師に憧れていました。大学は、埼玉大学工学部に進学しました。工学部では、副専攻プログラムがあり、一部の科目ではありますが、他の学部でも理学部数学科の講義を受けることができました。しかし、その後、埼玉大学では、転学部の制度が始まり、２年次に理学部数学科に転学しました。
転学後は、微分積分学、なかでも微分方程式やルベーグ積分論といった分野に興味をもちました。4年次、長澤壯之教授の研究室に配属され、非線型偏微分方程式の研究に興味をもちました。そこで、東北大学大学院の理学研究科数学専攻に進みました。
微分方程式はどういう関数が現れるかを予測するもの
研究分野の微分方程式についてお話しします。
関数 f(x)に対して、y = f(x)と書けたとして、x から x＋h までの微小変化率が「微分」に当たります。点 x から 点 x＋h までで、h の分だけ変化量があります。高さについては、yについての変化量は、f(x)から f(x＋h)までの分になります。「変化率」といっているので、f(x＋h) − f(x)／h という割り算をします。h が十分に小さく、また x にとても近いとき、x での微分が対応します。
微分方程式とはどういうものか、等速直線運動を例に見てみます。a地点から車が30km/hで1時間走ると、a地点から30km先に行くと予想できます。微分が関連する関係式を微分方程式といい、この等速直線運動を微分方程式で表すと、速度30km/h で時刻0の地点をaとして車が進むとき、 x(t)＝30t＋a となります。こうした微小変化率の関係式から、どういう関数が現れるかを導出する分野が微分方程式といえます。
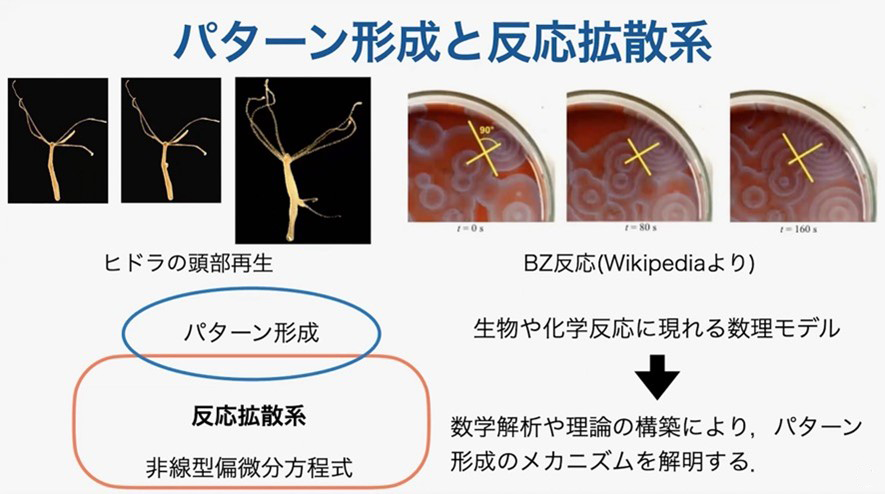
偏微分方程式は、空間 x と時間 t の微小変化率の関係式を表しており、その関係式を満たす関数を導出することが目的の一つにあります。反応拡散系の対象の一つにパターン形成があります。生きもの形態が形成されることをパターン形成といい、たとえば、ヒドラの頭の細胞をお腹に移植すると頭が生えてきます。こうしたパターン形成の現象を数学として捉えられないかと興味をもっています。
化学反応のベロウソフ・ジャボチンスキー（BZ）反応も、パターン形成で扱うことができます。BZ反応では、赤色の物質と白色の物質が、規則的かつ複雑なパターンを形づくっていきます。これを数学でどのように表されるかを考える必要があります。
反応方程式と拡散方程式を組み合わせる
反応拡散系を構成する、反応方程式と拡散方程式について補足します。
反応方程式については、化学反応式の例に見ていきます。Aという物質が、k1という割合でBという物質になるとします。Bがk-1の割合でAになるともいえます。（Aの時間変化率）＝ −k1A＋k-1B と表せます。左辺には時間微分が入るので、こうして化学反応式、つまり反応方程式を立てられます。
また、AとBが合わさってCができるとします。AとBが等しくkという割合でCに変わるとすると、（Aの時間変化率）＝（Bの時間変化率）＝ −kAB という方程式を立てられます。対してCについては （Cの時間変化率）＝ kAB という方程式を立てられます。
反応方程式の例としては、ほかに、人口・個体数の変動を表すロジスティック方程式、被食者・捕食者関係による個体数の変動を表すロトカ・ヴォルテラ方程式、また感染症モデルとしての反応方程式などがあります。
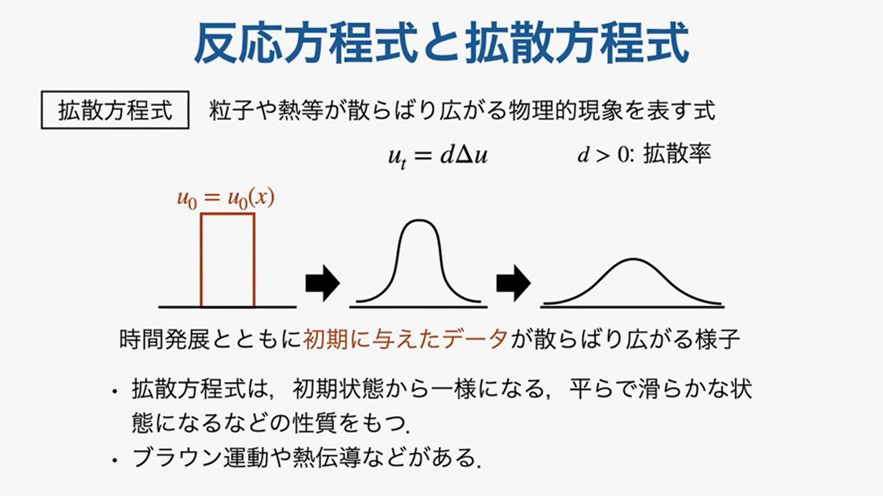
拡散方程式は、粒子や熱などが散らばり広がる物理現象を表す式といえます。初期状態として，このような台形のような関数が与えられたとすると、時間発展とともに関数のグラフは山型になって、さらに山型の部分は段々低くなり広がっていきます。このような変化から、拡散方程式はデータが散らばり広がる様子を表す方程式となっています。拡散方程式の例として、物理学のブラウン運動や熱伝導などの方程式を挙げられます。
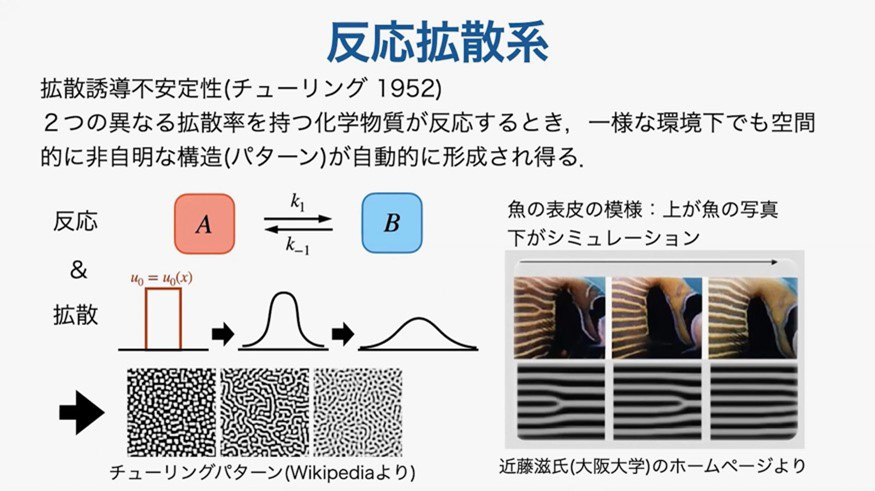
反応方程式と拡散方程式を組み合わせたものが反応拡散系です。反応拡散系の研究成果として、二つの異なる拡散のしかたをもつ化学物質が反応するとき、空間的に非自明なパターンが自己組織的に形成されうることがわかっています。大阪大学の近藤滋教授は、魚の表皮を傷つけて、縞模様ができる様子を観測し、生物の縞模様は生物の成長時のみにつくられるのではなく、化学反応でもつくられることを実証しています。
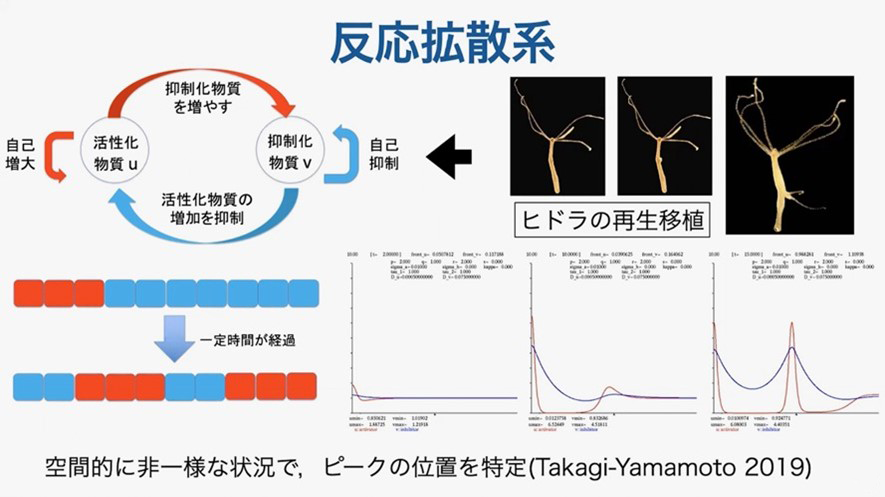
私の反応拡散系の研究成果としてはヒドラの再生移植を題材にしたものがあります。頭の細胞とおなかの細胞を分けて考えて、これを基に先行研究では、活性化物質と抑制化物質を想定して方程式が立てられました。私の研究では空間的に非一様な状況を想定し、変化が起きるピークの位置を具体的に特定することができました。特にピークの位置は、空間非一様性を表した方程式中の係数を用いて導くことができ、これにより空間非一様性がヒドラの頭部形成に影響することが分かりました。
現象と数理モデルを行き来する
偏微分方程式は社会において、いろいろな現象を数理モデルにしたり、数理モデルから現象へフィードバックしたりするなかで使われています。最近は、ネットワーク構造がどのように現れるかという問題がさかんに研究されており、反応拡散系の知見をどう応用できるか考えているところです。
哲学と数学に興味、教養学部から数学の道へ
大学入学前から哲学と数学に興味がありました。東京大学文科三類に入学し、語学、文学、数学寄りの哲学などに興味をもち学びました。その後、純粋数学への興味が高まり、進学振り分けを経て、3年次からは、教養学部の統合自然学科で学びました。その後、東京工業大学の大学院理学院数学系修士課程に進み、いまは博士課程で表現論という数学の一分野を研究しています。
数学は論理学化できるかを考える
いまの研究内容と異なりますが、数学基礎論や数理論理学のお話をします。
論理学とは、いくつかの公理や前提あるいは仮定と、推論規則を用いて定理を導きだすという思考過程を扱う学問です。数学と論理学をめぐって、「数学は論理学化することは可能か。一つの公理系のみで数学全体を記述することは可能か」と考える人が現れました。それに関連して、数学の論理学化の歴史と、ゲーデルの不完全性定理についてお話ししようと思います。
「この命題は証明できない」という命題について考えます。この命題を証明できるとすると「命題を証明できない」ということになり矛盾します。この命題を反証できる、つまり正しくないと証明できるとすると、「この命題は証明できる」ということになりますが、反証と証明が同時に成立することになるのでやはり矛盾します。ですがやはり命題自体は証明できない、という点でこの命題は真であると言えます。ゲーデルの第一不完全性定理は、このような証明も反証もできないが真であるような命題が数学の公理系でも構成される、ということを意味しています。
本題に入る前に、記号論理学で用いる基本的な記号を簡単に紹介します。否定「￢」、連言「∧」 、選言「∨」、条件法「⊃」などがあります。これらを用いて、推論規則を表現したり、命題の証明をしたりします。
では、数学は論理学化されうるのでしょうか。古代ギリシャのユークリッドは『原論』で定義・公理・公準を定め、そこから数々の命題を導き、平面幾何学を展開しました。時代を下ってドイツのゴットロープ・フレーゲ（1848-1925）は、『算術の基本法則』で素朴集合論をもとに数学の論理学化について論じました。これに対し、英国のバートランド・ラッセル（1872-1970）はフレーゲ宛の手紙で矛盾を指摘したのです(ラッセルのパラドクス)。フレーゲはこの指摘を解決できず、この流れを受けたラッセルが、英国のアルフレッド・ノース・ホワイトヘッド（1861-1947）と『プリンキピア・マテマティカ』で、数学の論理学化をはかったのでした。ドイツのダフィット・ヒルベルト（1862-1943）も、数学で真の命題は必ず証明できること、公理から形式化された推論をどこまで進めても、矛盾が出ることはないことを示すことにより、数学の完全性や無矛盾性を示そうとしました。
ゲーデルが不完全性定理を発表
これらの流れに打撃をあたえたのが、クルト・ゲーデル（1906-1978）による不完全性定理でした。ゲーデルは1931年の論文で、「自然数論を含む帰納的に記述できる公理系が、ω無矛盾であれば、証明も反証もできない命題が存在する」「自然数論を含む帰納的に記述できる公理が、無矛盾であれば、自身の無矛盾性を証明できない」とする二つの不完全性定理を示しました。
第一不完全性定理の証明について簡単に説明します。冒頭で述べた「この命題は証明できない」という命題を、「ゲーデル数」を用いて構成していきます。5個の公理系のセットからなる「ペアノ算術」の式について、否定「￢」は1、連言「∧」は2、選言「∨」は3……などと、記号をゲーデル数に置きなおします。記号の列で表される式のゲーデル数は、式に使われる記号の個数だけ小さい順に素数を並べ、それぞれの素数を対応する記号の(ゲーデル数)乗させて全て掛け合わせた数字とします。たとえば、 ∃x，x＝sy という式は「yの後継者（y＋1）であるxが存在する」となり、これをゲーデル数になおすと、26×317×514×717×117×1311×1719となります。
ここから、真だが証明も反証もできない命題をつくれます。ゲーデル数mをもつ式から、そのなかのゲーデル数19の変項に、mを表す数詞を代入したゲーデル数について考えます。m＝26×317×514×717×117×1311×1719とすると、ゲーデル数mは式 ∃x，x＝sy を表しています。∃x，x＝syの変項yをmに置きかえると、∃x，x＝sm となります。数としてのmは、sがm個のm＝ssssss……s0と記号化されるので、∃x，x＝sm であればsがm＋1個の ∃x，x＝sssssss……s0 と表されます。ここで各記号をゲーデル数に置きなおし、i番目に小さい素数をと置くと、sub（m, 19, m）＝ 26×317×514×717×117×1311×⋯×× となります。なお、ゲーデル数がmの式にyが入っていない場合、sub（m, 19, m）＝m となります。
Dem（x, y）＝「ゲーデル数xをもつ式系列は、ゲーデル数zをもつ式の証明になっている」という命題を考えます。式 ∀x￢Dem（x, sub（y, 19, y））のゲーデル数をnとすると、このとき、式 ∀x￢Dem（x, sub（n, 19, n））のゲーデル数は、Sub（n, 19, n）となります。この式をGとすると、Gは「どんなゲーデル数をもつ式系列でも、ゲーデル数 sub（n, 19, n）をもつ式の証明になっていない」ことを意味します。つまり、「Gは証明できない」ことを意味します。このGは「Gは証明できない」という命題になっています。
純粋数学とともにメタ数学の学びを
ゲーデルの不完全性定理は、人間の知の限界を示しているものではありません。命題が真であることとそれが証明可能であることの関係性や、数学を一つの公理系のみで記述することの限界性を示しているものです。
みなさんには、純粋数学とともに、今日とりあげたメタ数学ともよばれる数学基礎論それぞれの観点を学んでほしいと思っています。
