2020年9月7日
理化学研究所
慶應義塾大学
理化学研究所(理研)革新知能統合研究センター汎用基盤技術研究グループ数理科学チームの桑原知剛研究員と慶應義塾大学理工学部物理学科の齊藤圭司教授の共同研究チームは、量子力学的に運動する多数の粒子系(量子多体系[1])において、最低エネルギー状態(基底状態)が持つ「量子もつれ[2]」に関する新たな法則を発見しました。
本研究成果は、量子もつれに関する深い理解につながるだけでなく、量子多体系への数値計算によるアプローチに新しい知見をもたらし、さらには量子コンピュータ[3]や量子機械学習[4]を含む多方面の分野に有用な知見を与えると期待できます。
量子力学に従う粒子系を二つの領域に分けたとき、「領域間の量子もつれの大きさは、その境界の大きさとほぼ同じである」という予想を「量子もつれの境界則予想」といいます。この予想は、これまで粒子間に働く相互作用が小さく粒子が独立に運動しやすい(短距離の相関が存在する)状況では、数学的な証明が存在しました。しかし、相互作用の種類や大小によって、境界則成立の可否がどのように左右されるのかは、長年の重要な未解決問題の一つでした。
今回、共同研究チームは、エネルギーギャップ[5]を持つ広範囲の1次元量子多体系の基底状態で、量子もつれが高エネルギー状態よりも小さいことを意味する境界則を証明し、そのメカニズムを明らかにしました。これにより、これまで境界則に必要と考えられていた相互作用の短距離性の条件が本質ではないことが示され、長距離まで届く強い相互作用があっても境界則が成立することが初めて明らかになりました。
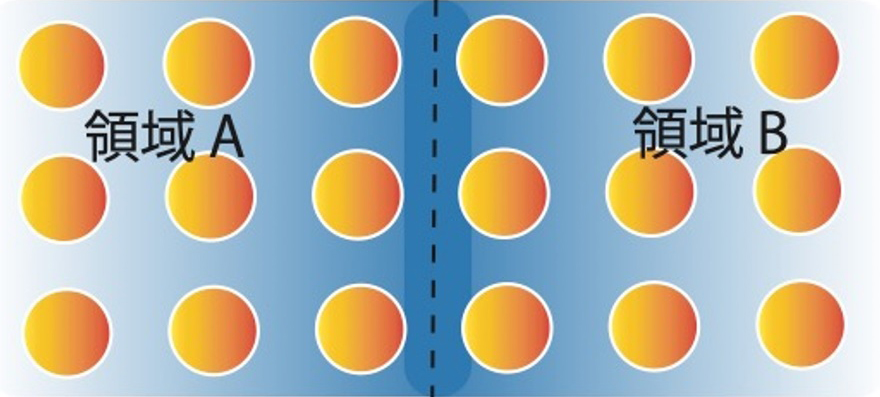
量子もつれにおける境界則のイメージ
(領域AとBの間の量子もつれの大きさは、その境界の大きさとほぼ等しい)
本研究は、オンライン科学雑誌『Nature Communications』(9月8日付)に掲載されました。
研究支援
本研究は、日本学術振興会(JSPS)科学研究費補助金若手研究「テンソルネットワーク形式を用いた量子多体問題の計算複雑性解析(研究代表者:桑原知剛)」、同基盤研究A「孤立量子多体系における熱力学第二法則(研究分担者:齊藤圭司)」の支援のもとに行われました。
1.背景
古典力学系[6]では、粒子の物理的状態は位置と運動量で表されます。粒子が多数になっても、それぞれの粒子の位置と運動量が分かれば、物理的な状態を記述することができます。また、粒子の間が十分に離れているために力が働いていない場合、各粒子の位置と運動量は、粒子1個の場合と全く同じ振る舞いを示します。つまり、古典力学系では、粒子間が十分に離れているときは粒子間に相関が存在しません。しかし、量子力学の世界では事情が違ってきます。異なる粒子の間に力が働かない(相互作用がない)状況になっても、粒子間に相関のある状態を維持させることができます。
例えば、二つの粒子にスピン[7]という自由度がある場合を考えます。スピンは、上向きと下向きを持つ小さな磁石と見なすこともできます。最初に、2個の粒子のスピンに相関のある状態を作り、一つ目の粒子を地球上に、二つ目の粒子を月面に移動させます。量子力学の世界では、粒子間が遠く離れていても有限の相関を持つ状態が存在し得ます。そのため、地球上の粒子のスピンで上向きを観測したとき、月面上の粒子のスピンも必ず上向きになる、あるいは逆に、地球上で下向きを観測したら月面上でも下向きになる、といった古典力学系ではあり得ないような相関を生み出すことができます。
このような性質のことを「量子もつれ(量子エンタングルメント)」といいます(図1)。近年進歩が目覚ましい量子コンピュータを用いた量子計算においては、この量子もつれが重要な役割を果たします。

図1 量子もつれのイメージ図
粒子1と粒子2が量子的にもつれた状態にあるとき、互いにどんな離れた場所にあっても、粒子1に対する測定は瞬時に粒子2の測定結果に影響を与える。
このように奇妙な性質を持つ量子もつれですが、粒子間の相互作用の種類や大小は、量子もつれの性質をどのように変化させるでしょうか。多数の粒子が集まった量子多体系における最低エネルギー状態(基底状態)を考えます。これまでの数値計算を含むさまざまな解析から、一般の量子多体系の基底状態が持つ量子もつれの大きさは、高エネルギーの状態と比較すると格段に小さいと予想されています。図2に示すように、量子もつれの大きさを示すエンタングルメントエントロピーという物理量は、多体系を半分に切ったときの領域Aと領域Bの間にある境界の面積にほぼ比例し、それ以上には大きくならないことから、領域Aと領域Bの間の量子もつれの大きさは、境界の大きさとほぼ同じであるという特徴を持ちます。そのため、この予想は「量子もつれの境界則予想」(あるいは面積則予想)と呼ばれています。量子もつれの境界則は、量子多体系を数値計算で研究する際の極めて重要な性質です。

図2 量子もつれにおける境界則のイメージ図
量子もつれの大きさを示す物理量エンタングルメントエントロピーは、多体系を半分に切ったときの境界の面積(濃い青の部分)にほぼ比例する。そのため、領域AとBの間の量子もつれの大きさは、その境界の大きさとほぼ等しい。
これまで、量子もつれの境界則予想は、粒子間に働く相互作用が小さく粒子が独立に運動しやすい(短距離の相関がある)状況では、数学的に証明されています。しかし、相互作用の種類や大小によって、境界則成立の可否がどのように左右されるのかは、長年の重要な未解決問題の一つでした。この問題を解決することは、量子もつれに関する深い理解につながるだけでなく、量子多体系を使った情報処理演算の効率化に直接的につながる重要な波及効果が期待されます。そこで共同研究チームは、自然界に働く最も一般的な相互作用を採用して、この問題に取り組みました。
2.研究手法と成果
自然界には、重力や電子間に働くクーロン力をはじめ、水分子のような極性分子の間にはたらく力、ミクロな磁石の構成分子の間に働く力など、遠くまで到達する力(長距離力)が存在します。近年では、冷却原子[8]を使って人工的に長距離力を操作することもできます。
共同研究チームは、長距離力で相互作用し、基底状態とそれよりエネルギーが高い状態との間に有限のエネルギーギャップがある1次元系を考えました。長距離力をもたらすポテンシャルの大きさは、距離に対してべき乗則に従ってゆっくりと小さくなり、その関数は距離 r の関数として「 ?−? (αは正の定数)」で表されます(図3)。

図3 長距離力の概念図(1次元)
長距離力は、距離に対してその大きさがべき乗則に従って小さくなるようなものを指し、減衰を特徴づける指数をαで表現する。このようなべき減衰の粒子間力は、自然界で普遍的に存在する。
一般的に、量子多体系における基底状態を正確に調べることは、最も難しい数学上の問題の一つです。そのため、共同研究チームは、基底状態を近似的に求めていく手法として、低いエネルギー状態を特定の状態に逐次射影していく手法(Approximate ground-state projection)を用いました。射影とは、ある量子状態がさまざまな状態の重ね合わせにあるときに、特定の状態に収縮させる操作のことです。ただし、射影行列(射影操作の数学的表現)を二つの領域(図2のA、Bの領域)の間の量子もつれの大きさが小さくなるような行列で表現することと、逐次射影による基底状態の近似計算の精度は、トレードオフの関係にあります。このトレードオフに起因する困難は、射影行列の構成を最適化すること、高いエネルギー状態を効率良く無視するための有効ハミルトニアン[9]を導入することで克服しました。
これらの数学的な手法を用いて、1次元系においては、一般的にα>2のときには、量子もつれの境界則が満たされることを見いだしました。さらに、量子多体系が2次形式[10]で書き下すことができる数値的に可解な系では、α>3/2でも境界則が満たされることが分かりました。これらの結果は、これまで境界則に必要と考えられていた相互作用の短距離性の条件が本質ではないことを示しており、強く長距離まで届く相互作用があっても境界則が成立することが初めて明らかになりました。
3.今後の期待
本研究により、量子もつれの境界則が広範囲な量子力学系で存在することが分かりました。このことは、広範囲の系で、基底状態を探る数値計算を探索できることを示しています。さらに本成果は、境界則成立が重要になるテンソルネットワーク[11]を使った量子アルゴリズムや、量子計算、量子機械学習など多くの分野に重要な知見をもたらすものと期待できます。
4.論文情報
| 論文題目: | Area law of non-critical ground states in 1D long-range interacting systems |
| 著者: | Tomotaka Kuwahara and Keiji Saito |
| 雑誌名: | Nature Communications 10.1038/s41467-020-18055-x |
5.補足説明
- [1]量子多体系
量子力学に従う多数の粒子が相互作用し合う系のこと。 - [2]量子もつれ(量子エンタングルメント)
異なる粒子の状態が、古典力学的には不可能な相関をもった状態。量子コンピュータを使った量子計算では、この量子的な相関が本質的な役割を果たす。 - [3]量子コンピュータ
古典コンピュータの並列計算を、量子もつれの性質などを使って高速に演算処理することができるコンピュータ。 - [4] 量子機械学習
量子コンピュータを用いて機械学習の問題を効率的に解くこと。一部の問題は量子コンピュータによって超高速化が達成できることが知られている。 - [5]エネルギーギャップ
量子力学系では、エネルギーがとびとびの値をとる。エネルギーギャップは、あるエネルギー状態とすぐ上のエネルギー状態の間のエネルギー幅のこと。 - [6]古典力学系
粒子の位置や速度が任意の時刻で確定しており、ニュートンの運動方程式に従う物理系を指す。私たちは古典力学的世界で情報をやり取りしている。 - [7]スピン
粒子の量子力学的効果を含んだ回転の自由度。磁石の微視的な状態。 - [8]冷却原子系
レーザーを用いて、多数の原子を冷却・捕捉した系。制御性に優れ、さまざまな量子多体系を実験的に実現できる。 - [9]有効ハミルトニアン
ハミルトニアンは系のエネルギーに対応する関数。有効ハミルトニアンは、特定の問題に対して現象をよく説明でき、かつ簡潔に記述されたハミルトニアンのこと。 - [10]2次形式
量子的な粒子の生成演算子と消滅演算子の対で記述されるようなハミルトニアンのクラス。 - [11]テンソルネットワーク
古典コンピュータを用いて、複雑な量子状態を効率的に計算するための数学的な記述方法。
6.発表者・機関窓口
<発表者> ※研究内容については発表者にお問い合わせください。
- 理化学研究所
革新知能統合研究センター 汎用基盤技術研究グループ 数理科学チーム
研究員 桑原 知剛 (くわはら ともたか)
問い合わせ先:https://aip.riken.jp/contactus/biz - 慶應義塾大学 理工学部物理学科
教授 齊藤 圭司 (さいとう けいじ)
<機関窓口>
- 理化学研究所 広報室 報道担当*
お問い合わせフォーム https://krs1.riken.jp/m/contact
*今般の新型コロナウイルス感染症対策として、理化学研究所では在宅勤務を実施しておりますので、問い合わせフォームにてお問い合わせ願います。 - 慶應義塾 広報室
TEL:03-5427-1541 FAX:03-5441-7640
E-mail:m-pr[at]adst.keio.ac.jp
※上記の[at]は@に置き換えてください。
掲載情報
マイナビニュース(9/10)、日刊工業新聞(10/7)、フジサンケイビジネスアイ(10/15)




